Random Graphs for Bayesian Graph Neural Networks

Real-world data is noisy. Graphs are constructed from data -> Observed graphs can contain errors. However, graphs are often treated as ground truth by graph learning algorithms

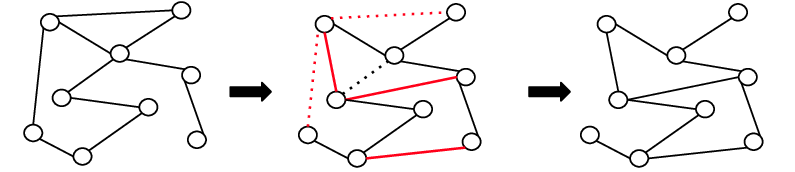
Idea : Generate graphs that look similar to the graph at hand.

The random graph model should be conditioned on $\mathcal{G}_{obs}$ and any additional information $\mathcal{D}$:

$\mathcal{G} \sim p(\mathcal{G} | \mathcal{G}_{obs}, \mathcal{D}).$

Multiple graphs can be sampled from $p(\mathcal{G} | \mathcal{G}_{obs}, \mathcal{D})$:

$\mathcal{G}_1 , \dots, \mathcal{G}_m \sim p(\mathcal{G} | \mathcal{G}_{obs}, \mathcal{D}).$

Those samples can be used in downstream graph learning tasks.

Our group developed several models for $p(\mathcal{G} | \mathcal{G}_{obs}, \mathcal{D})$ and demonstrated the benefits of this appraoch in various application settings, including node classification in low-labels regime, node classification in adversarial and recommender systems.

BGCN : Bayesian Graph Neural Networks

Parametric version with Stochastic Block Model

Authors:

• Yingxue Zhang
• Soumyasundar Pal
• Mark Coates (Prof. McGill University)

Non-parametric

Non-Parametric version with a correlation structure based on node embeddings distances.

Authors:

• Soumyasundar Pal
• Florence Regol
• Yingxue Zhang
• Mark Coates (Prof. McGill University)

Node Copying

Rabdom graph model based on first neighborhood structure sampling with replacement.

Authors:

• Florence Regol
• Soumyasundar Pal
• Yingxue Zhang
• Mark Coates (Prof. McGill University)