A Balanced Neuro-Symbolic Approach for Comonsense Abductive Logic
Although Large Language Models (LLMs) have demonstrated impressive formal reasoning abilities, they often break down when problems require complex proof planning. One promising approach for improving LLM reasoning abilities involves translating problems into formal logic and using a logic solver. Although off-the-shelf logic solvers are in principle substantially more efficient than LLMs at logical reasoning, they assume that all relevant facts are provided in a question and are unable to deal with missing commonsense relations. In this work, we propose a novel method that uses feedback from the logic solver to augment a logic problem with commonsense relations provided by the LLM, in an iterative manner. This involves a search procedure through potential commonsense assumptions to maximize the chance of finding useful facts while keeping cost tractable. On a collection of pure-logical reasoning datasets, from which some commonsense information has been removed, our method consistently achieves considerable improvements over existing techniques, demonstrating the value in balancing neural and symbolic elements when working in human contexts.
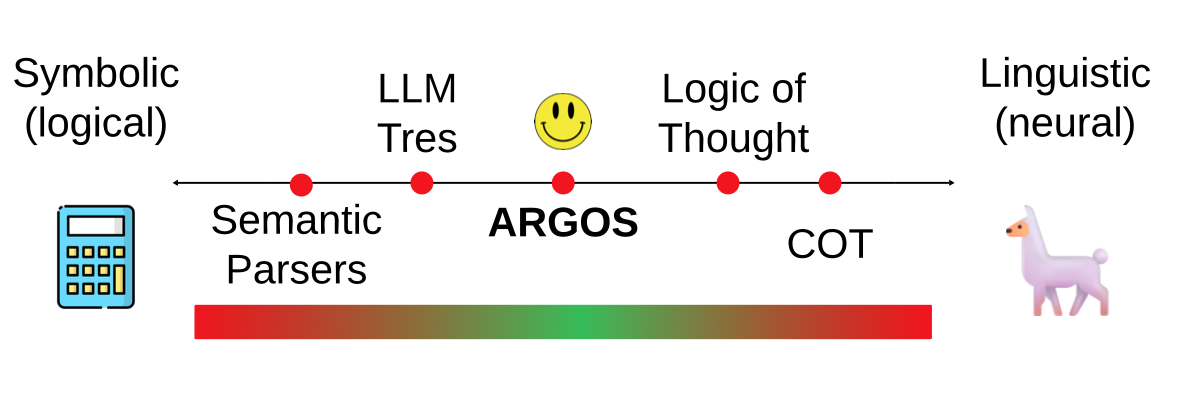
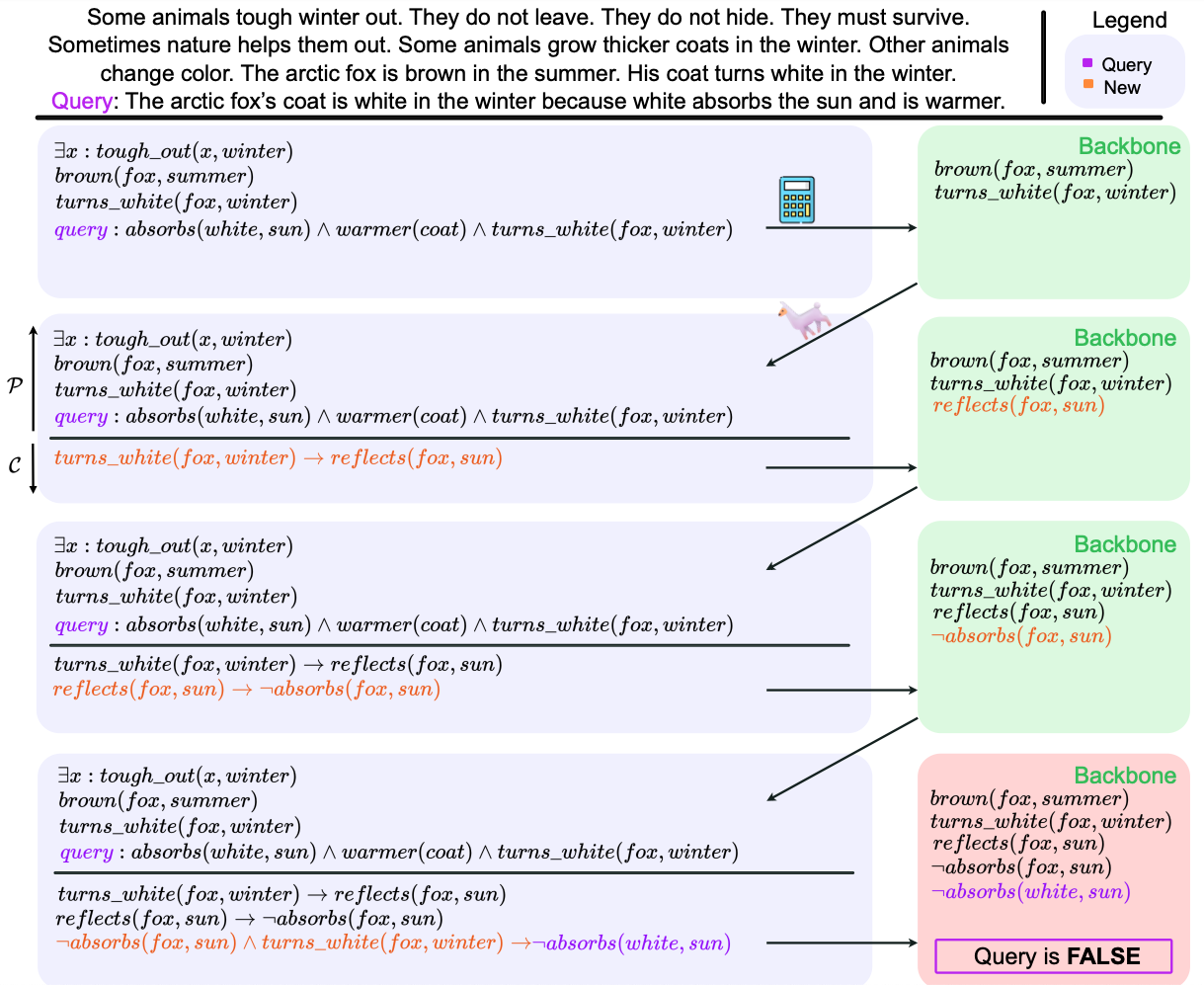
The existing approaches to logical reasoning approaches exist along a symbolic/linguistic spectrum, with methods such as Chain of Thought (COT) being on the extreme linguistic end, and Semantic Prasing methods (methods which translate the input to symbolic logic and directly attempt to solve via symbolic solvers) being on the extreme symbolic end. We note that symbolic methods tend to suffer the pitfall, namely lack of robustness to logical inconsistencies and human ambiguity. Similarly, linguistic methods all suffer from a tendency to hallucinate and to produce unfaithful reasonining. In this work, our aim is to produce a method which mixes both neural and linguistic reasoning componenents in such a way that each extreme's weaknesses are attenuated. In the Arctic Fox example below, we show an example in which the reasoning problem is simple for a human reasoner, becasue the human reasoner knows that white does not absorbe the sun. A direct translation to logic, however, does not inlcude this necessary but missing-from-the-input information, meaning that a symbolic solver can not deduce the truth of the query.

Abduction
In order to address the symbolic challenge of inconsistent or incomplete logical input, we do not apporoach the symbolic problem not in the classical deductive way; we instead use abductive logic. Abductive logical reasoning is the process of, given some logical context and a query, identifying the truthfulness of the query by first identifying the necessary additional logical propositions and then finally using symbolic logic to deduce the query's truth. This work focuses on developing a method which, using an LLM, can abduce propositions in such a way that the propositions are unlikely to ever be outright contradictory to the logical input, and in such a way that they are guaranteed to add concrete information to the problem. Since the generative LLM calls required to produce these propositions (single sentences) are cheap relative to a full COT, we can then generate many propositions according to these goals so that some of the generated propositions are somehow useful to the solving of the query.
Method
A high-level visualization of our method is below.
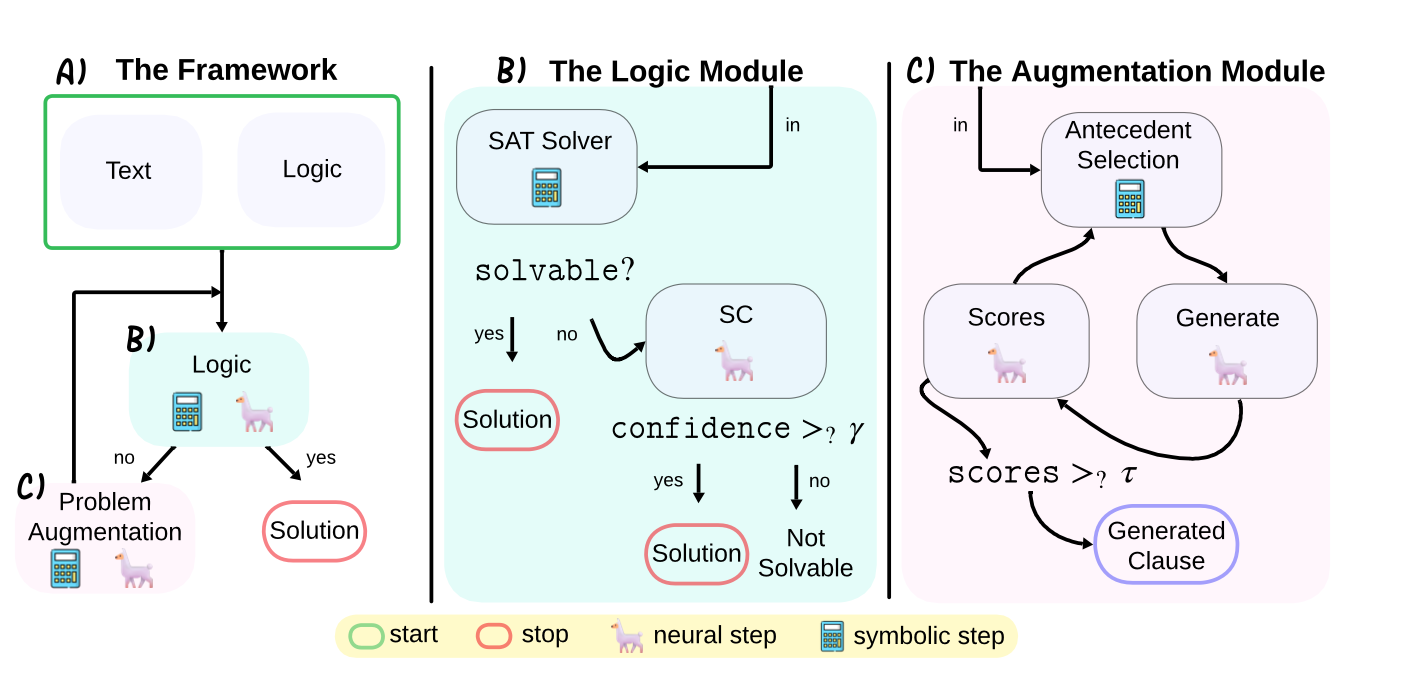
In the pane (A), we illustrate the general framework, in which the text (and its logical translation) are tested to see if the problem is already solvable. If it is, then the reasoning process is completed and we output solution. Otherwise, we abduce a new proposition, add it to the problem, and repeat. In (B), we describe how a problem's solvability is determined. First, a symbolic logical solver is employed (a SAT solver). If it determines the problem to be solvable, we exit. Otherwise, we also check if the problem is linguistically solvable, by checking the confidence of the linguistic solver (LLM): if the confidence is sufficiently high we consider the problem to be solvable. In (C), we depict the process by which we abduce propositions. First, we select up to 2 propositional variables which are in the problem and which are part of the backbone. The backbone of a problem is the set of propositional variables in the logic problem which are already fully deduced. Intuitively, this amounts to all he things about the problem which we know to be true. We select from among these variables according to a scoreing heuristic. Given two variables A, B, we construct a prompt "A and B implies ___", and allow the LLM to generate freely. This allows the LLM to introduce new, previously uninstantiated variables to the problem. Finally, we ensure that the generated propositions are not contradictory to either the input logic, or to commonsense in general, with a simple LLM-as-a-judge implementation. Below is an example of how this procedure will unfold, on the Arctic Fox exmaple, to reveal the necessary missing information in order to deduce the problem.
Citation
This project was accepted in ICLR 2026.
@inproceedings{ARGOS,
title={A Balanced Neuro-Symbolic Approach for Commonsense Abductive Logic},
author={Joseph Cotnareanu and Didier Chetelat and Yingxue Zhang and Mark Coates},
year={2026},
booktitle={Proc. Int. Conf. Learning Representations}
}